I. Introduction:

\(\bullet\) This system consists of six thermal units and based on IEEE 30 bus system \(\rightarrow\) please refer to our PF Library
\(\bullet\) The load demand is 2.834 per unit (p.u.). Some researchers could evaluate their proposed optimization algorithms with different load demands as in [3].
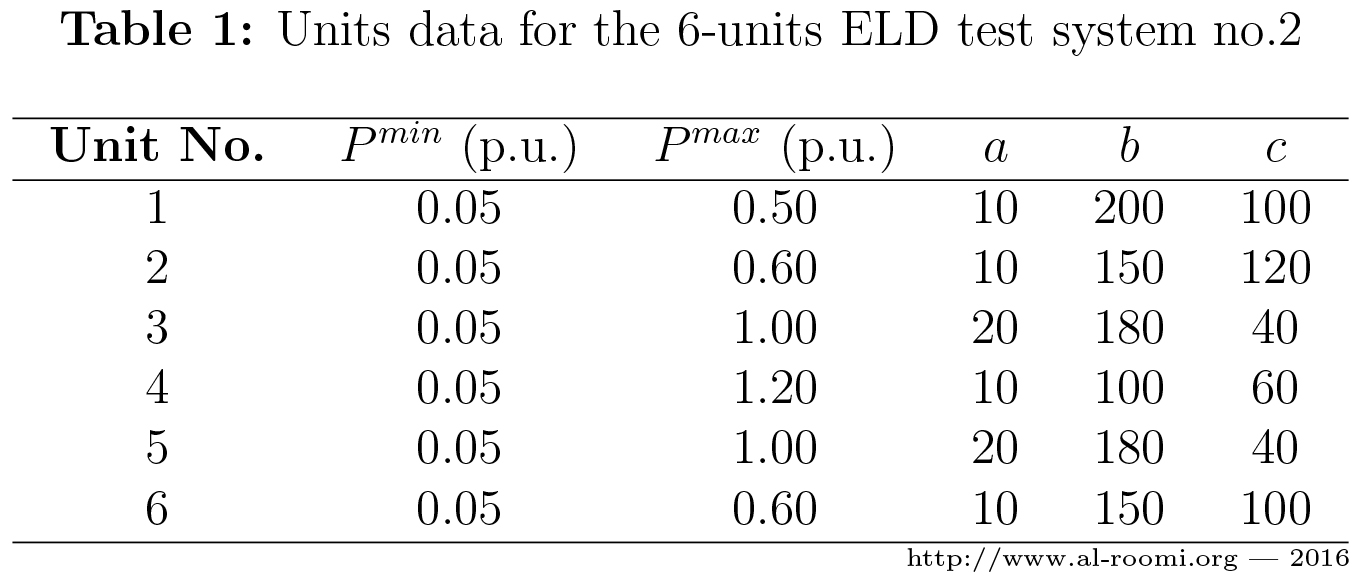
\(\bullet\) The fuel-cost function of this test system is modeled using the quadratic cost function as follows:

\(C_i\left(P_i\right) = a_i + b_i P_i + c_i P^2_i \) .......... \((1)\)

   where \(a_i\), \(b_i\), and \(c_i\) are the function coefficients and tabulated in Table 1.

\(\bullet\) The network losses are modeled using Kron's loss formula as follows:

\(P_L = \sum_{i=1}^{n} \sum_{j=1}^{n} P_i B_{ij} P_j + \sum_{i=1}^{n} B_{0i} P_i + B_{00}\) .......... \((2)\)

   where \(B_{ij}\), \(B_{0i}\), and \(B_{00}\) are called loss coefficients (or just B-coefficients) and listed below:

\(B_{ij}=\begin{bmatrix}
0.02180 & 0.01070 & -0.00036 & -0.00110 & 0.00055 & 0.00330 \\
0.01070 & 0.01704 & -0.00010 & -0.00179 & 0.00026 & 0.00280 \\
-0.00040 & -0.00010 & 0.02459 & -0.01328 & -0.01180 & -0.00790 \\
-0.00110 & -0.00179 & -0.01328 & 0.02650 & 0.00980 & 0.00450 \\
0.00055 & 0.00026 & -0.01180 & 0.00980 & 0.02160 & -0.00010 \\
0.00330 & 0.00280 & -0.00790 & 0.00450 & -0.00010 & 0.02978\end{bmatrix}\)

\(B_{0i} = 10^{-3} \times \left[0.010731,1.7704,-4.0645,3.8453,1.3832,5.5503\right]\)

\(B_{00} = 0.0014\)

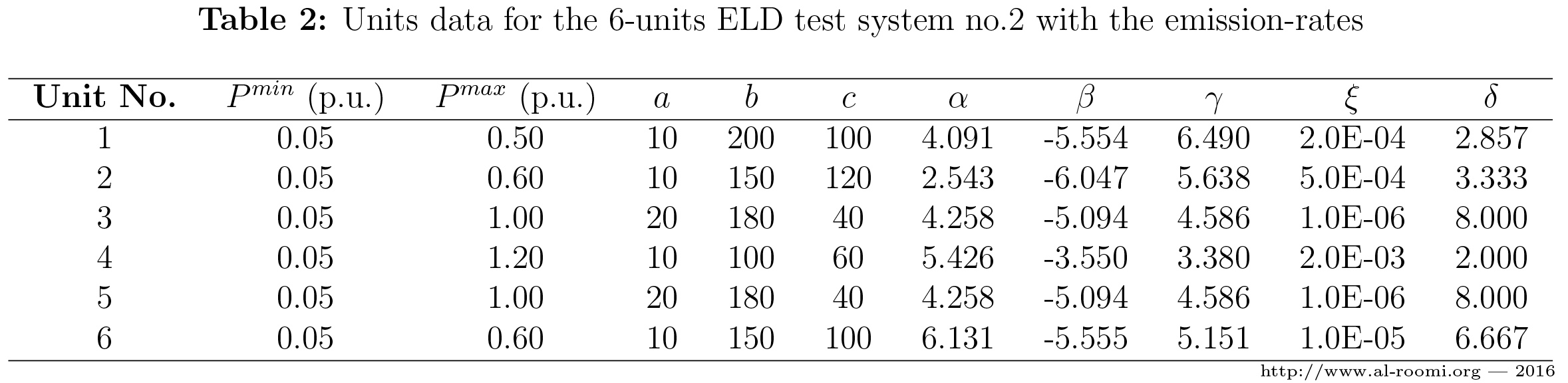
\(\bullet\) If the emission-rates are considered, then the following equation can be used to express these rates in the optimization problem:

\(E\left(\sum_{i=1}^n P_i\right) = \sum_{i=1}^n 10^{-2} \left(\alpha_i + \beta_i P_i + \gamma_i P^2_i \right) + \xi_i e^{\delta_i P_i}\) .......... \((3)\)

   where \(\alpha_i\), \(\beta_i\), \(\gamma_i\), \(\xi_i\), and \(\delta_i\) are the coefficients of the \(i\)th unit emission characteristics. Thus, Table 1 is expanded to Table 2 [4].

II. Files:

\(\bullet\) System Data (Text Format) [Download]

III. Citation Policy:

If you publish material based on databases obtained from this repository, then, in your acknowledgments, please note the assistance you received by using this repository. This will help others to obtain the same data sets and replicate your experiments. We suggest the following pseudo-APA reference format for referring to this repository:

Ali R. Al-Roomi (2016). Economic Load Dispatch Test Systems Repository [https://www.al-roomi.org/economic-dispatch]. Halifax, Nova Scotia, Canada: Dalhousie University, Electrical and Computer Engineering.

Here is a BiBTeX citation as well:

@MISC{Al-Roomi2016,
author = {Ali R. Al-Roomi},
title = {{Economic Load Dispatch Test Systems Repository}},
year = {2016},
address = {Halifax, Nova Scotia, Canada},
institution = {Dalhousie University, Electrical and Computer Engineering},
url = {https://www.al-roomi.org/economic-dispatch}
}

IV. References (Some selected papers that use this test system):

[1] M. A. Abido, “Environmental/Economic Power Dispatch Using Multiobjective Evolutionary Algorithms,” IEEE Trans. Power Syst., vol. 18, no. 4, pp. 1529–1537, Nov. 2003.
[2] R. T. F. A. King, H. C. S. Rughooputh, and K. Deb, “Evolutionary Multi-Objective Environmental/Economic Dispatch: Stochastic vs. Deterministic Approaches,” in Evolutionary Multi-Criterion Optimization (Third International Conference, EMO 2005, Guanajuato, Mexico, March 9-11, 2005. Proceedings), vol. 3410, C. A. C. Coello, A. H. Aguirre, and E. Zitzler, Eds. Springer Berlin Heidelberg, 2005, pp. 677–691.
[3] A. Bhattacharya and P. K. Chattopadhyay, “Application of Biogeography-based Optimization for Solving Multi-objective Economic Emission Load Dispatch Problems,” Electr. Power Components Syst., vol. 38, no. 3, pp. 340–365, Jan. 2010.
[4] S. Rajasomashekar and P. Aravindhababu, “Biogeography Based Optimization Technique for Best Compromise Solution of Economic Emission Dispatch,” Swarm Evol. Comput., vol. 7, pp. 47–57, Jun. 2012.